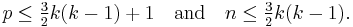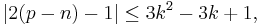Ragsdale conjecture
The Ragsdale conjecture is a mathematical conjecture that concerns the possible arrangements of real algebraic curves embedded in the projective plane. It was proposed by Virginia Ragsdale several years after 1900 and was disproved in 1979.[1]
Contents |
Background
Her dissertation dealt with Hilbert's sixteenth problem, which was proposed in the year 1900, along with 22 other unsolved problems of the 19th century. Ragsdale conjectured a particular upper bound on the number of topological circles of a certain type, along with the basis of evidence. The conjecture was held of high importance in the field of real algebraic geometry for nearly a century. Later Oleg Viro and Ilya Itenberg produced counterexamples to the Ragsdale conjecture, although the problem of finding a sharp upper bound remains unsolved.
Conjecture
Ragsdale's main conjecture is as follows.
Assume that an algebraic curve of degree 2k contains p even and n odd ovals. Ragsdale conjectured that
She also posed the inequality
and showed that the inequality could not be further improved. This inequality was later proved by Petrovsky.
Notes
- ^ Viro, Oleg Ya. (1980). "Кривые степени 7, кривые степени 8 и гипотеза Рэгсдейл [Curves of degree 7, curves of degree 8 and the hypothesis of Ragsdale]". Doklady Akademii Nauk SSSR 254 (6): 1306–1309. Translated in Soviet Mathematics - Doklady 22: 566–570. 1980.
References
- De Loera, Jesús; Frederick J. Wicklin (2006). "Virginia Ragsdale". Biographies of Women Mathematicians. http://www.agnesscott.edu/LRiddle/women/ragsdale.htm. Retrieved 2007-03-09.